The equilibrium between the FS and external
Moderators: hines, wwlytton, ramcdougal
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
The equilibrium between the FS and external
I am trying to simulate same example of extercellular in this paper"Computational Modeling of Three-Dimensional Electrodiffusion in
Biological Systems: Application to the Node of Ranvier".
The authors validated them work comparing to 1D Neuron including extracellular and intercellular. The authors used FH space as a limit of extracellular and beyond that there is an "The equilibrium between the FS and external world were governed by a variable rate constant.
I don not know how to do that variable rate constant using neuron. Can anyone help me please?
Biological Systems: Application to the Node of Ranvier".
The authors validated them work comparing to 1D Neuron including extracellular and intercellular. The authors used FH space as a limit of extracellular and beyond that there is an "The equilibrium between the FS and external world were governed by a variable rate constant.
I don not know how to do that variable rate constant using neuron. Can anyone help me please?
-
ted
- Site Admin
- Posts: 6389
- Joined: Wed May 18, 2005 4:50 pm
- Location: Yale University School of Medicine
- Contact:
Re: The equilibrium between the FS and external
Perhaps you refer to Lopreore et al. 2008, PMID 18556758. I have no idea how the authors did that. Does the paper contain a mathematical description of how the rate constant varied? Too bad the source code isn't available online. Have you contacted the authors to ask them?
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
Re: The equilibrium between the FS and external
Thank you for replying. Yes I referred the same reference you mentioned, and I don't have the Authers email. The variable rate constant is not clear in the paper, so I am trying to ask anyone can help me.
Anyone could help me please?
Anyone could help me please?
-
ted
- Site Admin
- Posts: 6389
- Joined: Wed May 18, 2005 4:50 pm
- Location: Yale University School of Medicine
- Contact:
Re: The equilibrium between the FS and external
Articles generally include the authors' contact information, which is typically provided near the abstract. Check the publisher's web site. If that doesn't work, do an internet search on their names or check the Society for Neuroscience member list. AFAIK, many if not most of the authors are still around and in the field.
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
Re: The equilibrium between the FS and external
Thank you for the suggestion, I will do research to find them.
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
Re: The equilibrium between the FS and external
If I have the rate of sodium and potassium (0.05 ms and 0.09 ms ) how can I write the new term which is responsible to depletion of potassium and add that term to the diffusion equation.. is it:
((Kbath-Ko)/tau)*volume/area surface.
volume is a whole external volume between axon and FH space
surface area is the area of external surrounded the FH space.
Is there example to work on it included the external and internal longitudinal diffusion for potassium and sodium ?
((Kbath-Ko)/tau)*volume/area surface.
volume is a whole external volume between axon and FH space
surface area is the area of external surrounded the FH space.
Is there example to work on it included the external and internal longitudinal diffusion for potassium and sodium ?
Re: The equilibrium between the FS and external
The rates you’ve given are in ms, so the rate of change
“((Kbath-Ko)/tau)*volume/area surface” is mM μm per ms (assuming the default mM for concentrations and μm for lengths). It looks like you are missing a distance?
We can use your time constants to specify the rate at which concentrations in the Frankenhaeuser–Hodgkin space equilibrate (Kbath-Ko)/tau), using rxd.Rate, shown below;
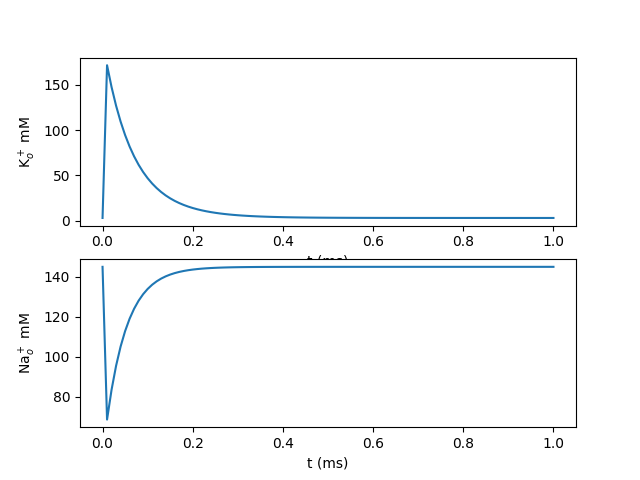
Here longitudinal diffusion is included with “d=...” in rxd.Species.
Membrane fluxes could be included in the model as in the Hogkin-Huxley example.
“((Kbath-Ko)/tau)*volume/area surface” is mM μm per ms (assuming the default mM for concentrations and μm for lengths). It looks like you are missing a distance?
We can use your time constants to specify the rate at which concentrations in the Frankenhaeuser–Hodgkin space equilibrate (Kbath-Ko)/tau), using rxd.Rate, shown below;
Code: Select all
from neuron import h, rxd
from neuron.units import mM, ms
from matplotlib import pyplot
h.load_file('stdrun.hoc')
# initial conditions and parameters
ki0, ko0 = 125.0 * mM, 3.0 * mM
nai0, nao0 = 10.0 * mM, 145.0 * mM
ktau = 0.09 * ms
natau = 0.05 * ms
# define the sections
axon = h.Section(name='axon')
axon.diam = 2.0
axon.nseg = 101
axon.L = 100
# Where -- the spaces needed (intracellular and Frankenhaeuser–Hodgkin)
cyt = rxd.Region([axon], nrn_region='i')
# define the F-H space as a Shell, a hollow cylinder extend from the diameter
# of the section (lo=1.0) to twice that diameter (hi=2.0)
fh = rxd.Region([axon], nrn_region='o', geometry=rxd.Shell(lo=1.0, hi=2.0))
# Who -- the species involved (K+ and Na+)
k = rxd.Species([cyt, fh], name='k', charge=1, d=2.6, initial=lambda nd:
ki0 if nd.region == cyt else ko0)
na = rxd.Species([cyt, fh], name='na', charge=1, d=1.8, initial=lambda nd:
nai0 if nd.region == cyt else nao0)
ki, ko, nai, nao = k[cyt], k[fh], na[cyt], na[fh]
# What -- the reaction (rates to restore F-H concentrations)
kdiff = rxd.Rate(ko, (ko0 - ko)/ktau)
nadiff = rxd.Rate(nao, (nao0 - nao)/natau)
# record some concentrations
t_vec = h.Vector().record(h._ref_t)
ko_vec = h.Vector().record(ko.nodes(axon(0.5))._ref_concentration)
nao_vec = h.Vector().record(nao.nodes(axon(0.5))._ref_concentration)
# initialize and run
h.finitialize(-70)
h.dt = 0.01
# perturb the initial state
ko.nodes(axon(0.5)).value = 200
na.nodes(axon(0.5)).value = 50
h.continuerun(1)
# plot the data
pyplot.subplot(2,1,1)
pyplot.plot(t_vec,ko_vec)
pyplot.xlabel('t (ms)')
pyplot.ylabel('K$^+_o$ mM')
pyplot.subplot(2,1,2)
pyplot.plot(t_vec,nao_vec)
pyplot.xlabel('t (ms)')
pyplot.ylabel('Na$^+_o$ mM')
pyplot.show()

Here longitudinal diffusion is included with “d=...” in rxd.Species.
Membrane fluxes could be included in the model as in the Hogkin-Huxley example.
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
Re: The equilibrium between the FS and external
Thank you for answer.
can you please answer those questions:
1-do I have add this the same tem to the potential equation and what do you expect the form of it.
2-Can you please write the same code with Neuron and not Python as file.hoc , because I did not installed Python. by this way I can your code using NEURON Simulator.
3- Can you give the example of external and internal concentration in file.hoc so I can modified it using NEURON.
Thank you in advance.
can you please answer those questions:
1-do I have add this the same tem to the potential equation and what do you expect the form of it.
2-Can you please write the same code with Neuron and not Python as file.hoc , because I did not installed Python. by this way I can your code using NEURON Simulator.
3- Can you give the example of external and internal concentration in file.hoc so I can modified it using NEURON.
Thank you in advance.
Re: The equilibrium between the FS and external
- These changes to concentrations in the Frankenhaeuser–Hodgkin would not directly alter the membrane potential, but may influence the currents for mechanisms you choose to put in the axon, via the Nernst potentials.
- This code above is written with NEURON. Python is the standard interface for NEURON and required to use the rxd module. Please try installing NEURON with Python, have a look at the quick start guide.
- The recommended way is to use the NEURON with the rxd Python module, but you could achieve a similar effect using a mod file, see example 6 in Expanding NEURON’s Repertoire of Mechanisms with NMODL.
-
ted
- Site Admin
- Posts: 6389
- Joined: Wed May 18, 2005 4:50 pm
- Location: Yale University School of Medicine
- Contact:
Re: The equilibrium between the FS and external
This thread will be split into two threads. The "new" thread will contain the posts on and after November 5.
Reason: The posts starting with November 5 are on a different topic than the earlier posts.
Basic Forum etiquette:
1. Do not make duplicate posts.
2. Questions or answers that diverge from the topic of an existing thread should not be appended to that thread. They should become the initial post of a new thread.
Violations of Forum etiquette can result in temporary suspension or banning from the Forum.
Reason: The posts starting with November 5 are on a different topic than the earlier posts.
Basic Forum etiquette:
1. Do not make duplicate posts.
2. Questions or answers that diverge from the topic of an existing thread should not be appended to that thread. They should become the initial post of a new thread.
Violations of Forum etiquette can result in temporary suspension or banning from the Forum.
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
Re: The equilibrium between the FS and external
Thank you for replaying, and I am sorry I did not mean to be disturbing.
I do not know the new topic where can post it to post it again at rigth place.
I do not know the new topic where can post it to post it again at rigth place.
-
ted
- Site Admin
- Posts: 6389
- Joined: Wed May 18, 2005 4:50 pm
- Location: Yale University School of Medicine
- Contact:
Re: The equilibrium between the FS and external
Don't worry about that--you don't have to repost anything. The new thread will go in this same discussion area, because it's about using rxd.
-
ahmed.hamzah
- Posts: 49
- Joined: Thu Jun 07, 2018 10:57 am
Re: The equilibrium between the FS and external
Dear adamjhn,
you said "1.These changes to concentrations in the Frankenhaeuser–Hodgkin would not directly alter the membrane potential, but may influence the currents for mechanisms you choose to put in the axon, via the Nernst potentials."
Can you tell me more about this mechanism please, and what is the governing equation behind?
you said "1.These changes to concentrations in the Frankenhaeuser–Hodgkin would not directly alter the membrane potential, but may influence the currents for mechanisms you choose to put in the axon, via the Nernst potentials."
Can you tell me more about this mechanism please, and what is the governing equation behind?
-
ted
- Site Admin
- Posts: 6389
- Joined: Wed May 18, 2005 4:50 pm
- Location: Yale University School of Medicine
- Contact:
Re: The equilibrium between the FS and external
That's a very good question. NEURON's computational engine can calculate ionic equilibrium potentials in the course of a simulation. If your model includes an NMODL-specified "ion accumulation mechanism" (a mechanism with a USEION statement that WRITEs the intra- or extracellular concentration of one or more ionic species), then by default NEURON's computational engine will automatically update the affected ionic concentrations and use the Nernst equation to recalculate the equilibrium potentials of those species in every affected segment the course of a simulation. rxd can also affect the concentrations of ionic species, but I must defer the discussion of that to Adam who knows a lot more about it than I do.
-
ramcdougal
- Posts: 270
- Joined: Fri Nov 28, 2008 3:38 pm
- Location: Yale School of Public Health
Re: The equilibrium between the FS and external
Similarly, NEURON automatically updates Nernst potentials for species defined using rxd. For more on the math governing Nernst Potentials, see this entry on Wikipedia. Ion current through a channel is typically proportional to the difference between the membrane potential and the corresponding Nernst potential.
Here's an example model with Hodgkin-Huxley dynamics and dynamic intracellular sodium and potassium.
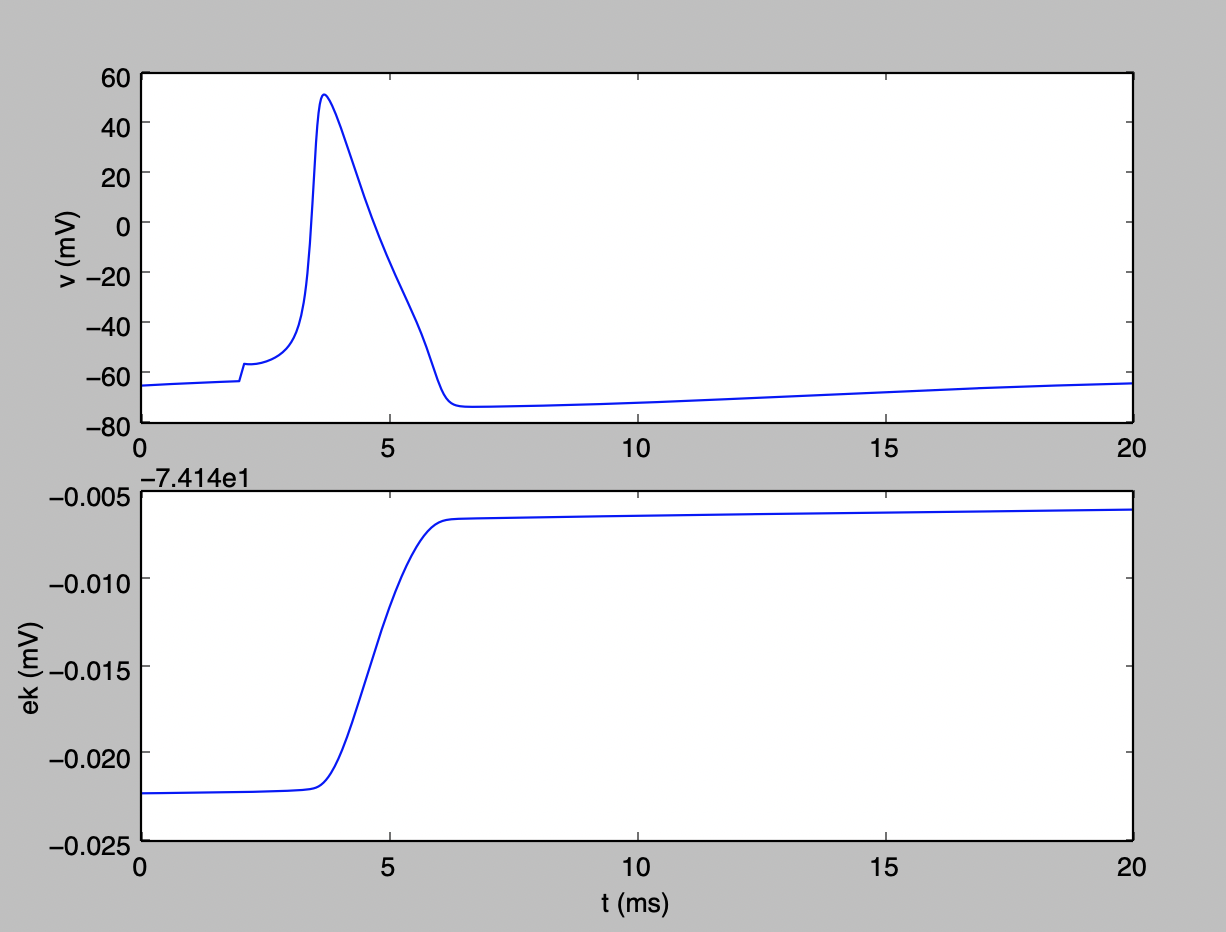
Note the y-axis on the lower graph is the offset relative to -74.14 mV. With potassium efflux, the potassium Nernst potential ek shifts slightly in a depolarizing direction.
Here's an example model with Hodgkin-Huxley dynamics and dynamic intracellular sodium and potassium.
Code: Select all
import matplotlib.pyplot as plt
from neuron import h, rxd
from neuron.units import ms, mV
h.load_file('stdrun.hoc')
soma = h.Section(name='soma')
soma.L = 20
soma.diam = 20
soma.insert('hh')
cyt = rxd.Region([soma], nrn_region='i')
k = rxd.Species(cyt, name='k', charge=1)
na = rxd.Species(cyt, name='na', charge=1)
iclamp = h.IClamp(soma(0.5))
iclamp.delay = 2
iclamp.dur = 0.1
iclamp.amp = 0.9
v = h.Vector().record(soma(0.5)._ref_v) # Membrane potential vector
t = h.Vector().record(h._ref_t) # Time stamp vector
ek = h.Vector().record(soma(0.5)._ref_ek)
h.finitialize(-65 * mV)
h.continuerun(20 * ms)
plt.figure()
plt.subplot(2, 1, 1)
plt.plot(t, v)
plt.ylabel('v (mV)')
plt.subplot(2, 1, 2)
plt.plot(t, ek)
plt.xlabel('t (ms)')
plt.ylabel('ek (mV)')
plt.show()

Note the y-axis on the lower graph is the offset relative to -74.14 mV. With potassium efflux, the potassium Nernst potential ek shifts slightly in a depolarizing direction.