Specify the Parameters

Step 5. Specify the parameters that will be adjusted

This involves two steps : specifying the model parameters that are to be adjusted, and constraining them.

A. Parameter specification

Proxy parameters

When we set up the MRF to optimize a function, we simply used its Parameters / Add Parameter button to add the function's parameters, one by one, to the list of parameters that it was to adjust. But now we're dealing with a model that has many sections, each with its own Ra, cm, and g_pas, and the MRF has to adjust them all. It also has to keep them equal over all sections.

One strategy for dealing with this problem is to create "proxies" for Ra, cm, and g_pas. We'd add these proxies to the MRF's parameter list. Then we would take advantage of the fact that NEURON's standard run system can be customized--we'd use a custom initialization that applies the same values to all sections.

Here's how :

First, we declare

  // proxies for NEURON's Ra, cm, g_pas
  Ri = 80    // ohm cm
  Cm = 1     // uf/cm2
  Rm = 1000  // ohm cm2

Then we write our own custom init() procedure that uses a forall loop to give all sections the same values of Ra, cm, and g_pas.

  proc init() {
    // optimizer adjusts Ri, Cm, Rm, but NEURON uses Ra, cm, g_pas
    forall {
      Ra = Ri
      cm = Cm
      g_pas = 1/Rm
    }
    finitialize(v_init)
    if (cvode.active()) {
      cvode.re_init()
    } else {
      fcurrent()
    }
    frecord_init()
  }

To simplify future code maintenance, we probably should put both of these code fragments into a single file called params.hoc.

To make use of params.hoc, we have to add a new load_file statement to init_iclampopt.hoc. The proxy variables have to exist before the MRF can use them, so params.hoc must be loaded before iclampfit.ses. Here's the new init_iclampopt.hoc :

  load_file("nrngui.hoc")
  load_file("rawmodel.ses")
  load_file("iclamp_rig.ses")
  load_file("rn.hoc")
  load_file("params.hoc")
  load_file("iclampfit.ses")

Before we can use the proxy variables with our MRF, we have to exit NEURON and restart with our new init_iclampopt.hoc

Testing the proxy parameters

Let's make sure the proxy parameters are doing what we think they should do. At the oc> prompt type

  rn()

This should return a numeric value of 5.6534218, i.e. the input resistance of our unoptimized model.

Now type

  forall print secname(), " ", g_pas

In each section, g_pas should be 0.001.

Next type

  Rm *= 2

Initializing the model will reduce g_pas in each section by a factor of 2, and increase the RN of the cell. Recalling that our rn() function does in fact initialize the model, we now type

  rn()

and get a returned value of 9.9076814 (the fact that RN didn't double tells us that the cell has significant electrotonic extent). And typing

  forall print secname(), " ", g_pas

confirms that g_pas is now 0.0005 everywhere.

Using the proxy parameters

Now we're ready to add Ri, Cm, and Rm to the MRF's parameter list. This is exactly the same as in the first tutorial.

Click on the MRF's Parameters / Add Parameter
This brings up a variable name browser (where have we seen that before?).
Click in the edit field of the variable name browser, type Ri, and then click on the Accept button.
Do the same for Cm and Rm

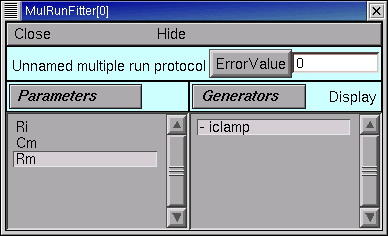
The MRF now looks like this, with Ri, Cm, and Rm in its left panel.

Save the MRF to a session file!

B. Viewing (and changing) parameter values

This too is the same as in the first tutorial : click on the MRF's Parameters / Parameter Panel

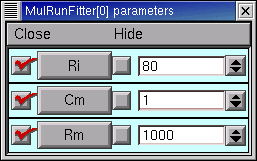
Let's change Rm and see what happens.
In the Parameter panel, we increase Rm to 10000

and then go back to the iclamp Run Fitness Generator and click on Error Value. This launches a new simulation

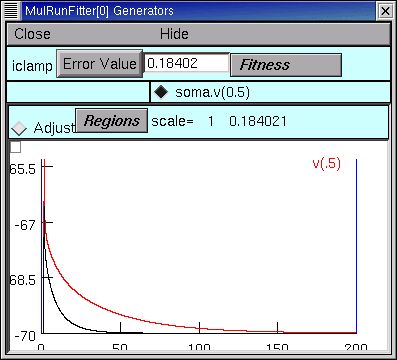
and we see that the new voltage trajectory (black trace) is closer to the experimental data (red trace), and the Error Value is smaller.

Before going any further, return Rm to 1000 to ensure that you're "in sync" with the remainder of this tutorial.

C. Constraining parameters

In the first tutorial, you will find a general discussion on the topic of constraining parameters. For this particular problem, we will take advantage of the fact that all three model parameters (Ri, Cm, and Rm) are positive definite and can be log scaled. We do this in exactly the same way as in the first tutoral.

Bring up the MRF's Domain panel by clicking on its Parameters / Domain Panel
In the MulRunFitter Domain panel click on
group attributes / positive definite limits
In the MulRunFitter Domain panel click on
group attributes / use log scale

Close the MulRunFitter Domain panel if you like; we can always bring it up again if we need it.

Save the MRF to a session file before proceeding any further!

The topic of "objective functions and optimization criteria" was briefly discussed in the first tutorial, and there's nothing more to say about it here.

Our next step is to optimize the model!

[ Outline | Previous | Next ]