Cell membrane with PMCA pump

[ziemek]

Hi!

I would like to model PMCA pump on the cell membrane. In the Calcium wave example there is a serca pump model:

Code: Select all

cyt_er_membrane = rxd.Region(h.allsec(), geometry=rxd.DistributedBoundary(1))
serca = rxd.MultiCompartmentReaction(ca[cyt], ca[er], gserca / ((kserca / (1000. * ca[cyt])) ** 2 + 1), membrane=cyt_er_membrane, custom_dynamics=True)

But it is created between 2 inner regions of the cell.

How can I model pump which pumps Calcium out of the cell ?

[ramcdougal]

Are you trying to do this with a network model or a single cell? Do you care what happens to the extracellular concentration or do you want to treat that as constant?

A way of doing this is to an rxd.Extracellular domain and to use the rxd.membrane() geometry for the plasma membrane. The following example pumps out at a rate proportional to the current intracellular calcium concentration:

Code: Select all

import matplotlib.pyplot as plt
from neuron import h, rxd
from neuron.units import mV, ms
h.load_file('stdrun.hoc')

soma = h.Section(name='soma')
soma.diam = soma.L = 10

ecs = rxd.Extracellular(-20, -20, -20, 20, 20, 20, dx=10)
cyt = rxd.Region([soma], name='cyt', nrn_region='i')
mem = rxd.Region([soma], name='mem', geometry=rxd.membrane())

ca = rxd.Species([cyt, ecs],
                 d=1,  # with single section and nseg=1 only affects extracellular
                 name='ca',
                 charge=2,
                 initial=lambda node: 1e-3 if node.region==cyt else 0)

e = 1.60217662e-19
scale = 1e-14 / e

# rate constant is in terms of molecules/um2 ms
ca_pump = rxd.MultiCompartmentReaction(ca[cyt], ca[ecs], ca[cyt] * scale, 
                                       custom_dynamics=True,
                                       membrane_flux=True,
                                       membrane=mem)

t = h.Vector().record(h._ref_t)
ca_vec = h.Vector().record(soma(0.5)._ref_cai)
ca_vec2 = h.Vector().record(ca[ecs].node_by_location(5, 0, 0)._ref_value)
v = h.Vector().record(soma(0.5)._ref_v)

h.finitialize(-65 * mV)
h.continuerun(100 * ms)

plt.subplot(2, 1, 1)
plt.plot(t, ca_vec * 1000, label='inside')
plt.plot(t, ca_vec2 * 1000, label='outside')
plt.ylabel('[Ca] (uM)')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(t, v)
plt.ylabel('v (mV)')
plt.xlabel('t (ms)')
plt.show()

The membrane_flux=True indicates that we must respect the fact that the pump, by moving ions, is by definition generating a current. Some people prefer to consider the corresponding effects on membrane potential to be cancelled out by other, not explicitly modeled currents. In that case, you could set this to False (then membrane potential would stay constant.)

If you're wondering why membrane potential is so affected (it should get down to -112 mV), it's only because we didn't add any other currents (not even leak).

[ziemek]

Thank you for the fast and very detailed response! :)

Currently I don't care so much about extracellular space so I wonder if there is any other way to pump out Ca2+? Because I assume that the extracellular computation maybe much more expensive.

Also I would like to specify explicitly 2 reactions:

• ca2 + pmca <-> pmca_ca (Ca2+ binding with PMCA pump)

• pmca_ca <-> pmca + ca_out (pumping out Ca2+ and PMCA returns to the initial conformation)

So I created this code:

Code: Select all

pmca = rxd.Species(regions=cyt, initial=PMCA_CONCENTRATION * nM)
pmca_ca = rxd.Species(regions=cyt, initial=0)

pmca_ca_reaction = rxd.Reaction(ca + pmca, pmca_ca, kf1, kb1)
pmca_ca__pmca_reaction = rxd.Reaction(pmca_ca, pmca, kf_out, 0)  # CaOut

But in this case pmca pump is just "floating" inside the compartment as any other buffer, so is there any way to create a species and attach it into the membrane?

[adamjhn]

Sorry for the late reply.

You’re right that rxd.Extracellular may be more expensive but you could easily include an outside region paralleling the cell (nrn_region=’o’) with minimal overhead cost. Additionally you can use a Parameter, so its value won’t be updated.

With a recent improvement on the development version (https://github.com/neuronsimulator/nrn), which allows MultiCompartmentReaction sources (and destinations) to be on both the ‘i’ or ‘o’ side of the membrane, the pump mechanisms you described could be implemented as follows;

Code: Select all

import matplotlib.pyplot as plt
from neuron import h, rxd
from neuron.units import mV, ms, nM, mM
h.load_file('stdrun.hoc')
plt.ion()
soma = h.Section(name='soma')
soma.diam = soma.L = 10
PMCA_CONCENTRATION = 50 * nM
kf = 1e9             # forward rate [ca]*[pmca]*kf molecules/um**2/ms 
kr, kcat = 1e5, 1e5  # reverse and catalytic rates [bound]*kr molecules/um**2/ms 

cyt = rxd.Region(soma, name='cyt', nrn_region='i')
ecs = rxd.Region(soma, name='ecs', nrn_region='o', geometry=rxd.Shell(1, 2))
mem = rxd.Region(soma, name='mem', geometry=rxd.membrane())

ca = rxd.Species(cyt , d=1, name='ca', charge=2, initial=60*nM)
caecs = rxd.Parameter(ecs, name='ca', charge=2)

pcma = rxd.Species(mem, name='pcma', initial=PMCA_CONCENTRATION)
pcma_bound = rxd.Species(mem, name='pcma_bound', initial=0)


# define species on regions for the multicompartment reactions
cai, cao, unbound, bound = ca[cyt], caecs[ecs], pcma[mem], pcma_bound[mem]

# reversibly bind ca to the pump and generate a current 
pcma_bind = rxd.MultiCompartmentReaction(cai + unbound, bound, kf, kr,
                                         membrane_flux=True, membrane=mem)

# remove ca and returns the pump to the unbound state
# note: this reaction cannot generate a current because the extracellular
# (nrn_region='o') concentration (represented by a parameter) does not change. 
pcma_extrue = rxd.MultiCompartmentReaction(bound, unbound + cao, kcat,
                                           membrane=mem)

t = h.Vector().record(h._ref_t)
ca_vec = h.Vector().record(soma(0.5)._ref_cai)
unbound_vec = h.Vector().record(unbound.nodes._ref_value)
bound_vec = h.Vector().record(bound.nodes._ref_value)
v = h.Vector().record(soma(0.5)._ref_v)

h.finitialize(-65 * mV)
h.continuerun(100 * ms)

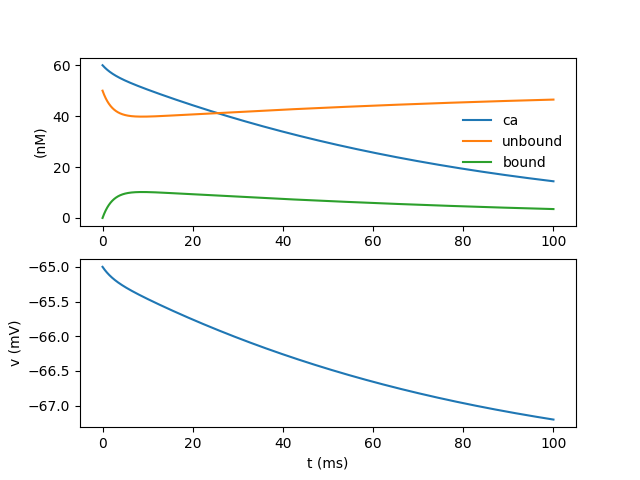
plt.subplot(2, 1, 1)
plt.plot(t, ca_vec / nM, label='ca')
plt.plot(t, unbound_vec / nM, label='unbound')
plt.plot(t, bound_vec / nM, label='bound')
plt.ylabel('(nM)')
plt.legend(frameon=False)
plt.subplot(2, 1, 2)
plt.plot(t, v)
plt.ylabel('v (mV)')
plt.xlabel('t (ms)')
plt.show()

[Feanor]

Hi ramcdougal,

Could you explain the derivation of the scale factor here? Why is the electron charge in the factor? I would have guessed Avogadro's number would have something to do with it. Why 1e-14? um2 is 1e-12 m2, is that related?

Code: Select all

e = 1.60217662e-19
scale = 1e-14 / e

# rate constant is in terms of molecules/um2 ms
ca_pump = rxd.MultiCompartmentReaction(ca[cyt], ca[ecs], ca[cyt] * scale, 
                                       custom_dynamics=True,
                                       membrane_flux=True,
                                       membrane=mem)

Thanks!