|
|
Spatial discretization reduced the cable equation, a partial
differential equation with derivatives in space and time, to a set of ordinary
differential equations with first order derivatives in time. Selection of an
integration method to solve these equations is guided by concerns of stability,
accuracy, and efficiency (Hines and Carnevale 1995).
NEURON offers the user a choice of two stable implicit integration methods:
backward Euler, and a variant of Crank-Nicholson (C-N). Backward Euler is the
default because of its robust numerical stability properties. Backward Euler
can be used with extremely large time steps in order to find the steady-state
solution for a linear ("passive") system. It produces good qualitative results
even with large time steps, and it works even if some or all of the equations
are strictly algebraic relations among states.
A method which is more accurate for small time steps is available by setting
the global parameter secondorder to 2. NEURON then uses a variant of
the C-N method, in which numerical error is proportional to
 .
Both of these are implicit integration methods, in which all current balance
equations must be solved simultaneously. The backward Euler algorithm does not
resort to iteration to deal with nonlinearities, since its numerical error is
proportional to
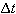anyway. The special feature of the C-N variant
is its use of a staggered time step algorithm to avoid iteration of nonlinear
equations (see 3.3.1 Efficiency). This converts the current
balance part of the problem to one that requires only the solution of
simultaneous linear equations.
Although the C-N method is formally stable, it is sometimes plagued by
spurious large amplitude oscillations (see Fig. 7 in Hines and Carnevale
(1995)). This occurs when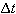
is too large, as may occur in models
that involve fast voltage clamps or that have compartments which are coupled by
very small resistances. However, C-N is safe in most situations, and it can be
much more efficient than backward Euler for a given accuracy.
These two methods are almost identical in terms of computational cost per time
step (see 3.3.1 Efficiency). Since the current balance equations
have the structure of a tree (there are no current loops), direct gaussian
elimination is optimal for their solution (Hines 1984). This takes exactly thesame number of computer operations as would be required for an unbranched cable
with the same number of compartments.
For any particular problem, the best way to determine which is the method of
choice is to compare both methods with several values of
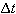to see
which allows the largest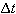
consistent with the desired accuracy.
In performing such trials, one must remember that the stability properties of a
simulation depend on the entire system that is being modeled. Because
of interactions between the "biological" components and any "nonbiological"
elements, such as stimulators or voltage-clamps, the time constants of the
entire system may be different from those of the biological components alone.
A current source (perfect current clamp) does not affect stability because it
does not change the time constants. Any other signal source imposes a load on
the compartment to which it is attached, changing the time constants and
potentially requiring use of a smaller time step to avoid numerical
oscillations in the C-N method. The more closely a signal source approximates
a voltage source (perfect voltage clamp), the greater this effect will be.
|
Nonlinear equations generally need to be solved iteratively to maintain
second order correctness. However, voltage dependent membrane properties,
which are typically formulated in analogy to Hodgkin-Huxley (HH) type channels,
allow the cable equation to be cast in a linear form, still second order
correct, that can be solved without iterations. A direct solution of the
voltage equations at each time step
using the
linearized membrane current I(V,t) = G
(V - E) is sufficient as long
as the slope conductance G and the effective reversal potential E
are known to second order at time
 .
HH type channels are easy to solve at
since the
conductance is a function of state variables which can be computed using a
separate time step that is offset by
with respect to the
voltage equation time step. That is, to integrate a state from
to
we only require a second order correct value for the
voltage dependent rates at the midpoint
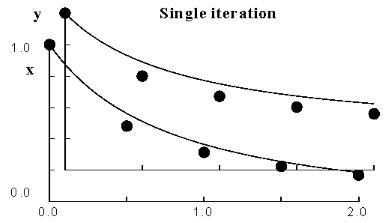
Figure 3.5 contrasts this approach with the common technique of replacing
nonlinear coefficients by their values at the beginning of a time step. For HH
equations in a single compartment, the staggered time grid approach converts
four simultaneous nonlinear equations at each time step to four independent
linear equations that have the same order of accuracy at each time step. Since
the voltage dependent rates use the voltage at the midpoint of the integration
step, integration of channel states can be done analytically in just a single
addition and multiplication operation and two table lookup operations. While
this efficient scheme achieves second order accuracy, the tradeoff is that the
tables depend on the value of the time step and must be recomputed whenever the
time step changes.
|
|
Figure 3.5 A. The equations
 ,
are computed using the Crank-Nicholson method.
Here
and
are determined using their values at time t.
|
|
Figure 3.5 B. Staggered time steps yield decoupled linear equations.
is determined using
x(t)
, after which
is determined using
.
|
|
Neuronal architecture can also be exploited to increase computational
efficiency. Since neurons generally have a branched tree structure with no
loops, the number of arithmetic operations required to solve the cable equation
by Gaussian elimination is exactly the same as for an unbranched cable with the
same number of compartments. That is, we need only O(N) arithmetic operations
for the equations that describe N compartments connected in the form of a tree,
even though standard Gaussian elimination generally takes O(N3)
operations to solve N equations in N unknowns. The tremendous efficiency
increase results from the fact that, in a tree, one can always find a leaf
compartment i that is connected to only one other compartment j,
so that: 1) the equation for compartment i (Eq. 3a) involves only the voltages in compartments i and j, and2) the voltage in leaf compartment i is involved only in the equations for compartments i and j (Eq. 3a and b). |
| aii Vi + aij Vj = bi | (3a) |
| aji Vi + ajj Vj + [terms from other compartments] = bj | (3b) |
| Using Eq. 3a to eliminate the Vi term from Eq. 3b, which requires O(1) (instead of N) operations, gives Eq. 4 and leaves N-1 equations in N-1 unknowns. |
| a'jj Vj + [terms from other compartments] = b'j | (4) |
|
where
a'jj = ajj
(aij aji / aii)
and
b'j = bj
(bi aji / aii).
This strategy can be applied until there is only one equation in one unknown.
Assume that we know the solution to these N-1 equations, and in particular
that we know Vj. Then we can find Vi from
|
|
Efficient Gaussian elimination requires an ordering that can be found by a
simple algorithm: choose the equation with the current minimum number of terms
as the equation to use in the elimination step. This minimum degree ordering
algorithm is commonly employed in standard sparse matrix solver packages. For
example, NEURON's "Matrix" class uses the matrix library written by Stewart and
Leyk (1994). This and many other sparse matrix packages are freely available
on the Internet at http://www.netlib.org
.
|
|
|
|
Address questions and inquiries to Michael Hines or Ted Carnevale
Digital preprint of "The NEURON Simulation Environment" by M.L. Hines and N.T. Carnevale,
Neural Computation, Volume 9, Number 6 (August 15, 1997), pp. 1179-1209.
Copyright © 1997 by the Massachusetts Institute of Technology, all rights reserved. |