|
|
|
Every nerve simulation program solves for the longitudinal spread of
voltage and current by approximating the cable equation as a series of
compartments connected by resistors (Fig. 3.4 and Eq. 2). The sum of all the
compartment areas is the total membrane area of the whole nerve.
Unfortunately, it is usually not clear at the outset how many compartments
should be used. Both the accuracy of the approximation and the computation
time increase as the number of compartments used to represent the cable
increases. When the cable is "short," a single compartment can be made to
adequately represent the entire cable. For long cables or highly branched
structures, it may be necessary to use a large number of compartments.
This raises the question of how best to manage all the parameters that exist
within these compartments. Consider membrane capacitance, which has a
different value in each compartment. Rather than specify the capacitance of
each compartment individually, it is better to deal in terms of a single
specific membrane capacitance which is constant over the entire cell and have
the program compute the values of the individual capacitances from the areas of
the compartments. Other parameters such as diameter or channel density may
vary widely over short distances, so the graininess of their representation may
have little to do with numerically adequate compartmentalization.
Although NEURON is a compartmental modeling program, the specification of
biological properties (neuron shape and physiology) has been separated from the
numerical issue of compartment size. What makes this possible is the notion of
a section, which is a continuous length of unbranched cable. Although
each section is ultimately discretized into compartments, values that can vary
with position along the length of a section are specified in terms of a
continuous parameter that ranges from 0 to 1 (normalized distance). In this
way, section properties are discussed without regard to the number of segments
used to represent it. This makes it easy to trade off between accuracy and
speed, and enables convenient verification of the numerical correctness of
simulations.
|
|
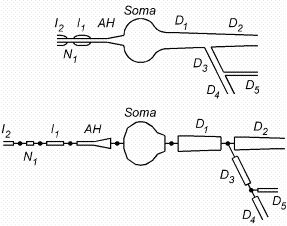
| Figure 3.2. Top: cartoon of a neuron indicating the approximate boundaries between biologically significant structures.. The left hand side of the cell body (Soma) is attached to an axon hillock (AH) that drives a myelinated axon (myelinated internodes Ii alternating with nodes of Ranvier Ni). From the right hand side of the cell body originates a branched dendritic tree (Di). Bottom: how sections would be employed in a NEURON model to represent these structures. |
|
Sections are connected together to form any kind of branched tree structure.
Fig. 3.2 illustrates how sections are used to represent biologically
significant anatomical features. The top of this figure is a cartoon of a
neuron with a soma that gives rise to a branched dendritic tree and an axon
hillock connected to a myelinated axon. Each biologically significant
component of this cell has its counterpart in one of the sections of the NEURON
model, as shown in the bottom of Fig. 3.2: the cell body (Soma), axon
hillock (AH), myelinated internodes (Ii), nodes of
Ranvier (Ni), and dendrites (Di). Sections
allow this kind of functional/anatomical parcellation of the cell to remain
foremost in the mind of the person who constructs and uses a NEURON model.
To accommodate requirements for numerical accuracy, NEURON represents each
section by one or more segments of equal length (Figs. 3.3 and 3.4).
The number of segments is specified by the parameter nseg,
which can have a different value for each section.
At the center of each segment is a node, the location where the
internal voltage of the segment is defined. The transmembrane currents over
the entire surface area of a segment are associated with its node. The nodes
of adjacent segments are connected by resistors.
It is crucial to realize that the location of the second order correct voltage
is not at the edge of a segment but rather at its center, i.e. at its
node. This is the discretization method employed by NEURON. To allow
branching and injection of current at the precise ends of a section while
maintaining second order correctness, extra voltage nodes that represent
compartments with 0 area are defined at the section ends. It is possible to
achieve second order accuracy with sections whose end nodes have nonzero area
compartments. However, the areas of these terminal compartments would have to
be exactly half that of the internal compartments, and extra complexity would
be imposed on administration of channel density at branch points.
|
|
|
|
|
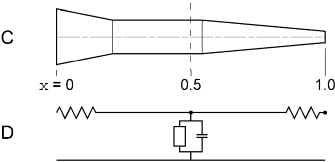
Figure 3.3 A. Cartoon of an unbranched neurite (thick lines) that is to be represented by a section in a NEURON model. Computer-assisted morphometry generates a file that stores successive measurements of diameter (thin circles) centered at x, y, z coordinates (thin crosses). B. Each adjacent pair of diameter measurements (thick circles) becomes the parallel faces of a truncated cone or frustum, the height of which is the distance between the measurement locations. The outline of each frustum is shown with thin lines, and a thin centerline passes through the central axis of the chain of solids. |
|
|
Based on the position of the nodes, NEURON calculates the values of internal
model parameters such as the average diameter, axial resistance, and
compartment area that are assigned to each segment. Figs. 3.3 and 3.4 show how
an unbranched portion of a neuron, called a neurite (Fig. 3.3A), is represented
by a section with one or more segments. Morphometric analysis generates a
series of diameter measurements whose centers lie on the midline of the neurite
(thin axial line in Fig. 3.3B). These measurements and the path lengths
between their centers are the dimensions of the section, which can be regarded
as a chain of truncated cones or frusta (Fig. 3.3C).
|
|
|
|
|
Figure 3.3 C. The centerline has been straightened so the faces of adjacent frusta are flush with each other. The scale underneath the figure shows the distance along the midline of the section in terms of the normalized position parameter x. The vertical dashed line at D. Electrical equivalent circuit of the section as represented by a single segment (nseg = 1). The open rectangle includes all mechanisms for ionic (non-capacitive) transmembrane currents. |
|
|
Distance along the length of a section is discussed in terms of the normalized
position parameter x. That is, one end of the section
corresponds to x = 0 and the other end to x = 1. In Fig.
3.3C these locations are depicted as being on the left and right hand ends of
the section. The locations of the nodes and the boundaries between segments
are conveniently specified in terms of this normalized position parameter. In
general, a section has nseg segments that are demarcated by evenly
spaced boundaries at intervals of 1 / nseg. The nodes at the centers
of these segments are located at x = (2 i - 1) / 2
nseg where i is an integer in the range [1, nseg]. As
we shall see later, x is also used in specifying model parameters or
retrieving state variables that are a function of position along a section (see
4.4 Range variables).
The special importance of x and nseg lies in the fact that
they free the user from having to keep track of the correspondence between
segment number and position on the nerve. In early versions of NEURON, all
nerve properties were stored in vector variables where the vector index was the
segment number. Changing the number of segments was an error prone and
laborious process that demanded a remapping of the relationship between the
user's mental image of the biologically important features of the model, on the
one hand, and the implementation of this model in a digital computer, on the
other. The use of x and nseg insulates the user from the
most inconvenient aspects of such low-level details.
When nseg = 1 the entire section is lumped into a single compartment.
This compartment has only one node, which is located midway along its length,
i.e. at x = 0.5 (Fig. 3.3C and D). The integral of the surface area
over the entire length of the section (0 <= x <= 1) is used to
calculate the membrane properties associated with this node. The values of the
axial resistors are determined by integrating the cytoplasmic resistivity along
the paths from the ends of the section to its midpoint (dashed line in Fig.
3.3C). The left and right hand axial resistances of Fig. 3.3D are evaluated
over the x intervals [0, 0.5] and [0.5, 1], respectively.
|
|
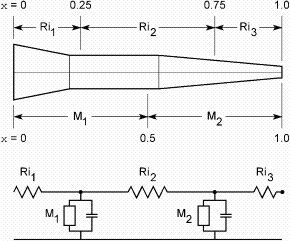
| Figure 3.4. How the neurite of Fig. 3.3 would be represented by a section with two segments (nseg = 2). Now the electrical equivalent circuit (bottom) has two nodes. The membrane properties attached to the first and second nodes are based on neurite dimensions and biophysical parameters over the x intervals [0, 0.5] and [0.5, 1], respectively. The three axial resistors are computed by integrating cytoplasmic resistance over the intervals shown. |
|
Fig. 3.4 shows what happens when nseg = 2. Now NEURON breaks the
section into two segments of equal length that correspond to x
intervals [0, 0.5] and [0.5, 1]. The membrane properties over these intervals
are attached to the nodes at 0.25 and 0.75, respectively. The three axial
resistors Ri1, Ri2 and Ri3 are computed
from the cytoplasmic resistivity and neurite
dimensions over the x intervals [0, 0.25], [0.25, 0.75], and [0.75, 1].
|
|
|
|
Address questions and inquiries to Michael Hines or Ted Carnevale
Digital preprint of "The NEURON Simulation Environment" by M.L. Hines and N.T. Carnevale,
Neural Computation, Volume 9, Number 6 (August 15, 1997), pp. 1179-1209.
Copyright © 1997 by the Massachusetts Institute of Technology, all rights reserved. |