- pnt
- get_loc · get_segment · has_loc · loc
Point Processes and Artificial Cells¶ ↑
- Description:
- Built-in POINT_PROCESS models and ARTIFICIAL_CELL models are listed above. The user may add other classes of those types using mod files. Some properties and functions that are available for all POINT_PROCESS models are described under General.
See also
General¶ ↑
-
pnt.get_loc()¶ ↑ - Syntax:
x = pnt.get_loc() sec = h.cas() h.pop_section()
- Description:
pnt.get_loc()pushes the section containing the POINT_PROCESS instance, pnt, onto the section stack (makes it the currently accessed section, readable viah.cas()), and returns the position (ranging from 0 to 1) of the POINT_PROCESS instance. The section stack should be popped when the section is no longer needed.
See also
Warning
Due to the manipulation of NEURON’s section stack, this function is best avoided in new Python code; use
get_segment()instead.
-
pnt.get_segment()¶ ↑ - Syntax:
pyseg = pnt.get_segment()- Description:
- Returns the segment containing the point process.
From a segment object one can get the
section with
pyseg.secand the position withpyseg.x. If the point process is not located anywhere, the return value is None.
Example:
>>> s = h.Section(name='s') >>> ic = h.IClamp(s(0.5)) >>> ic.get_segment() s(0.5)
Warning
Segment objects become invalid if nseg changes. Discard them as soon as possible and do not keep them around.
-
pnt.loc()¶ ↑ - Syntax:
pnt.loc(section(x))- Description:
Moves the POINT_PROCESS instance, pnt, to the center of the segment
section(x).The syntax
pnt.loc(x, sec=section)will also work.
-
pnt.has_loc()¶ ↑ - Syntax:
b = pnt.has_loc()- Description:
- Returns 1 if the POINT_PROCESS instance, pnt, is located in some section, otherwise, 0.
-
class
IClamp¶ ↑ - Syntax:
stimobj = h.IClamp(section(x))delay -- msdur -- msamp -- nAi -- nA- Description:
See <nrn src dir>/src/nrnoc/stim.mod
Single pulse current clamp point process. This is an electrode current so positive amp depolarizes the cell. i is set to amp when t is within the closed interval delay to delay+dur. Time varying current stimuli can be simulated by setting delay=0, dur=1e9 and playing a vector into amp with the
play()Vectormethod.
Note
In HOC,
delaywas known asdel, but this had to be renamed for Python asdelis a Python keyword.
-
class
AlphaSynapse¶ ↑ - Syntax:
syn = h.AlphaSynapse(section(x))syn.onset --- mssyn.tau --- mssyn.gmax --- umhosyn.e --- mVsyn.i --- nA- Description:
See <nrn src dir>/src/nrnoc/syn.mod. The comment in this file reads:
synaptic current with alpha function conductance defined by i = g * (v - e) i(nanoamps), g(micromhos); where g = 0 for t < onset and g = gmax * (t - onset)/tau * exp(-(t - onset - tau)/tau) for t > onset this has the property that the maximum value is gmax and occurs at t = delay + tau.
-
class
VClamp¶ ↑ - Syntax:
vc = h.VClamp(section(x))vc.dur[0],vc.dur[1],vc.dur[2]vc.amp[0],vc.amp[1],vc.amp[2]vc.gain, vc.rstim, vc.tau1, vc.tau2vc.i- Description:
Two electrode voltage clamp.
See <nrn src dir>/src/nrnoc/vclmp.mod. The comment in this file reads:
Voltage clamp with three levels. Clamp is on at time 0, and off at time dur[0]+dur[1]+dur[2]. When clamp is off the injected current is 0. Do not insert several instances of this model at the same location in order to make level changes. That is equivalent to independent clamps and they will have incompatible internal state values.
The control amplifier has the indicated gain and time constant. The input amplifier is ideal.
tau2 gain +-|\____rstim____>to cell -amp --'\/`-------|/ | |----||--- |___ __|-----/|___from cell `'`' \| tau1The clamp has a three states which are the voltage input of the gain amplifier, the voltage output of the gain amplfier, and the voltage output of the measuring amplifier. A good initial condition for these voltages are 0, 0, and v respectively.
This model is quite stiff. For this reason the current is updated within the solve block before updating the state of the clamp. This gives the correct value of the current on exit from
fadvance(). If we didn’t do this and instead used the values computed in the breakpoint block, it would look like the clamp current is much larger than it actually is since it doesn’t take into account the change in voltage within the timestep, ie equivalent to an almost infinite capacitance. Also, because of stiffness, do not use this model except withsecondorder=0.This model makes use of implementation details of how models are interfaced to neuron. At some point I will make the translation such that these kinds of models can be handled straightforwardly.
Note that since this is an electrode current model v refers to the internal potential which is equivalent to the membrane potential v when there is no extracellular membrane mechanism present but is v+vext when one is present. Also since i is an electrode current, positive values of i depolarize the cell. (Normally, positive membrane currents are outward and thus hyperpolarize the cell)
-
class
SEClamp¶ ↑ - Syntax:
clampobj = h.SEClamp(section(x)).dur1 .dur2 .dur3 -- ms.amp1 .amp2 .amp3 -- mV.rs -- MOhm.vc -- mV.i -- nA- Description:
Single electrode voltage clamp with three levels.
See <nrn src dir>/src/nrnoc/svclmp.mod. The comment in this file reads:
Single electrode Voltage clamp with three levels. Clamp is on at time 0, and off at time dur1+dur2+dur3. When clamp is off the injected current is 0. The clamp levels are amp1, amp2, amp3. i is the injected current, vc measures the control voltage) Do not insert several instances of this model at the same location in order to make level changes. That is equivalent to independent clamps and they will have incompatible internal state values. The electrical circuit for the clamp is exceedingly simple:
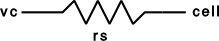
Note that since this is an electrode current model v refers to the internal potential which is equivalent to the membrane potential v when there is no extracellular membrane mechanism present but is v+vext when one is present. Also since i is an electrode current, positive values of i depolarize the cell. (Normally, positive membrane currents are outward and thus hyperpolarize the cell)
This model is careful to ensure the clamp current is properly computed relative to the membrane voltage on exit from fadvance and can therefore be used with time varying control potentials. Like
VClampit is suitable forplay()ing a Vector into the control potential.The following example compares the current that results from clamping an action potential originally elicited by a current pulse.
from neuron import h # setup for three simulations s1 = h.Section(name='s1') s2 = h.Section(name='s2') s3 = h.Section(name='s3') for sec in [s1, s2, s3]: sec.insert('hh') sec.L = sec.diam = 3 c1 = h.IClamp(s1(0.5)) c2 = h.SEClamp(s2(0.5)) c3 = h.VClamp(s3(0.5)) c1.dur = 0.1 c1.amp = 0.3 c2.dur1 = 1 c2.rs = 0.01 c3.dur[0] = 1 # record an action potential ap = h.Vector() ap.record(s1(0.5)._ref_v) h.finitialize(-65) while h.t < 1: h.fadvance() # do the three cases while playing the recorder ap apc = ap.c() # unfortunately, cannot play into two variables, so clone it ap.play_remove() ap.play(c2._ref_amp1, h.dt) apc.play(c3._ref_amp[0], h.dt) h.finitialize(-65) while h.t < 0.4: h.fadvance() print('%11g %11g %11g %11g %11g %11g' % (s1.v, s2.v, s3.v, c1.i, c2.i, c3.i))
Output:
-38.9151 -65 -64.9987 0.3 -8.57284e-06 6.08992e-06 -13.2522 -38.9181 -39.9175 0.3 0.299966 0.28846 12.0382 -13.2552 -14.2775 0.3 0.299999 0.299544 36.8707 12.0352 11.0258 0.3 0.3 0.299976 35.8703 36.8677 35.876 0 0.299999 0.299835 35.9246 35.8703 35.8698 0 3.53006e-05 0.0116979 36.944 35.9246 35.9218 0 1.88827e-06 0.000592712 38.5089 36.944 36.9039 0 1.91897e-06 7.48624e-05 40.1456 38.5089 38.4464 0 1.60753e-06 -2.12119e-05 41.5259 40.1456 40.0795 0 1.15519e-06 -6.25541e-05 42.5135 41.5259 41.4695 0 7.13443e-07 -6.92656e-05 43.1106 42.5135 42.4725 0 3.47428e-07 -5.86879e-05 43.3834 43.1106 43.0853 0 6.29392e-08 -4.51288e-05 43.4093 43.3834 43.3711 0 -1.57826e-07 -3.50748e-05 43.2531 43.4093 43.407 0 -3.34836e-07 -2.94783e-05 42.9618 43.2531 43.2582 0 -4.82874e-07 -2.71847e-05
-
class
APCount¶ ↑ - Syntax:
apc = h.APCount(section(x))apc.thresh --- mVapc.napc.time --- msapc.record(vector)- Description:
Counts the number of times the voltage at its location crosses a threshold voltage in the positive direction. n contains the count and time contains the time of last crossing.
If a
Vectoris attached to the apc, then it is resized to 0 when the INITIAL block is called and the times of threshold crossing are appended to the Vector. apc.record() will stop recording into the vector. The apc is not notified if the vector is freed but this can be fixed if it is convenient to add this feature.
-
class
ExpSyn¶ ↑ - Syntax:
syn = h.ExpSyn(section(x))syn.tau --- ms decay time constantsyn.e -- mV reversal potentialsyn.i -- nA synaptic current- Description:
Synapse with discontinuous change in conductance at an event followed by an exponential decay with time constant tau.
i = G * (v - e) i(nanoamps), g(micromhos); G = weight * exp(-t/tau)
The weight is specified by the
weightfield of aNetConobject.This synapse summates.
-
class
Exp2Syn¶ ↑ - Syntax:
syn = h.Exp2Syn(section(x))syn.tau1 --- ms rise timesyn.tau2 --- ms decay timesyn.e -- mV reversal potentialsyn.i -- nA synaptic current- Description:
Two state kinetic scheme synapse described by rise time tau1, and decay time constant tau2. The normalized peak condductance is 1. Decay time MUST be greater than rise time.
The kinetic scheme
A -> G -> bath 1/tau1 1/tau2
produces a synaptic current with alpha function like conductance (if tau1/tau2 is appoximately 1) defined by
i = G * (v - e) i(nanoamps), g(micromhos); G = weight * factor * (exp(-t/tau2) - exp(-t/tau1))
The weight is specified by the
weightfield of aNetConobject. The factor is defined so that the normalized peak is 1. If tau2 is close to tau1 this has the property that the maximum value is weight and occurs at t = tau1.Because the solution is a sum of exponentials, the coupled equations for the kinetic scheme can be solved as a pair of independent equations by the more efficient cnexp method.
This synapse summates.
-
class
NetStim¶ ↑ - Syntax:
s = h.NetStim()s.interval ms (mean) time between spikess.number (average) number of spikess.start ms (most likely) start time of first spikes.noise ---- range 0 to 1. Fractional randomness.0 deterministic, 1 intervals have negexp distribution.- Description:
Generates a train of presynaptic stimuli. Can serve as the source for a NetCon. This NetStim can also be be triggered by an input event. i.e serve as the target of a NetCon. If the stimulator is in the on=0 state and receives a positive weight event, then the stimulator changes to the on=1 state and goes through its burst sequence before changing to the on=0 state. During that time it ignores any positive weight events. If, in the on=1 state, the stimulator receives a negative weight event, the stimulator will change to the off state. In the off state, it will ignore negative weight events. A change to the on state immediately causes the first spike.
Fractional noise, 0 <= noise <= 1, means that an interval between spikes consists of a fixed interval of duration (1 - noise)*interval plus a negexp interval of mean duration noise*interval. Note that the most likely negexp interval has duration 0.
Since NetStim sends events, the proper idiom for specifying it as a source for a NetCon is
from neuron import h nc = h.NetStim() ns = h.NetCon(nc, target...)
That is, do not use
nc._ref_yas the source for the netcon.
Warning
Prior to version 5.2.1 an attempt was made to make the mean start time (noise > 0) correspond to the value of start. However since it is not possible to simulate events occurring at t < 0, these spikes were generated at t=0. Thus the mean start time was not start and the spikes at t=0 did not obey negexp statistics. For this reason, beginning with version 5.2.1 the semantics of start are the time of the most likely first spike and the mean start time is start + noise*interval.
-
class
PatternStim¶ ↑ - Syntax:
s = h.PatternStim()s.play(tvec, gidvec)s.fake_output --- 0 or 1- Description:
- The spikeout pairs (t, gid) resulting from a parallel network simulation can become the stimulus for any single cpu subnet. Only spikes with gid’s that are not owned by this process and are associated with NetCon instances created by pc.gid_connect(gid, target) are delivered when s.fake_output == 0. If s.fake_output == 1, all spikes associated with gid’s specified by pc.gid_connect(gid, target) including those gid’s owned by this process are delivered.
Note
Must retain references to the tvec and gidvec vectors to avoid use of freed memory since PatternStim does not increment the reference count for those vectors. Calling s.play() with no arguments turns off the PatternStim.
- Example:
from neuron import h pc = h.ParallelContext() #Model cell = h.IntFire1() cell.refrac = 0 # no limit on spike rate pc.set_gid2node(0, pc.id()) pc.cell(0, h.NetCon(cell, None)) # generates a spike with gid=0 nclist = [pc.gid_connect(i, cell) for i in range(4)] #note gid=0 recursive connection for i, nc in enumerate(nclist): nc.weight[0] = 2 # anything above 1 causes immediate firing for IntFire1 nc.delay = 1 + 0.1*i # incoming (t, gid) generates output (t + 1 + 0.1*gid, 0) # Record all spikes (cell is the only one generating output spikes) out = [h.Vector() for _ in range(2)] pc.spike_record(-1, out[0], out[1]) #PatternStim tvec = h.Vector(range(10)) gidvec = h.Vector(range(10)) # only 0,1,2 go to cell ps = h.PatternStim() ps.play(tvec, gidvec) #Run pc.set_maxstep(10.) h.finitialize() pc.psolve(7) for i, tsp in enumerate(out[0]): print ("%g %d" %(tsp, int(out[1][i])))
- Output:
Notice that 2.1 is the first output because (0, 0) is discarded by PatternStim because fake_fire=0 and gid=0 is owned by this process. (1, 1) is the first spike that gets passed into a NetCon (with delay 1.1) so the first output spike is generated at 2.2 and that spike gets recursively regenerated every 1.0 ms. PatternStim spikes with gid > 3 are discarded. .. code-block:
2.1 0 3.1 0 3.2 0 4.1 0 4.2 0 4.3 0 5.1 0 5.2 0 5.3 0 6.1 0 6.2 0 6.3 0
-
class
IntFire1¶ ↑ - Syntax:
c = h.IntFire1()c.tau --- ms time constantc.refrac --- ms refractory period. Minimum time between events is refracc.m --- state variablec.M --- analytic value of state at current time, t- Description:
A point process that is equivalent to an entire integrate and fire cell.
An output spike event is sent to all the NetCon instances which have this pointprocess instance as their source when m >= 1 If m(t0) = m0 and an input event occurs at t1 then the value of m an infinitesimal time before the t1 event is exp(-(t1 - t0)/tau). After the input event m(t1) = m(t1) + weight where weight is the weight of the NetCon event. Input events are ignored for refrac time after the spike output event.
During the refractory period, m = 2. At the end of the refractory period, m = 0. During the refractory period, the function M() returns a value of 2 for the first 0.5 ms and -1 for the rest of the period. Otherwise it returns exp((t-t0)/tau)
-
class
IntFire2¶ ↑ - Syntax:
c = h.IntFire2()c.taum --- ms membrane time constantc.taus -- ms synaptic current time constantc.ib -- constant current inputc.m --- membrane state variablec.M --- analytic value of state at current time, tc.i --- synaptic current state variablec.I --- analytic value of synaptic current.- Description:
A leaky integrator with time constant taum driven by a total current that is the sum of { a user-settable constant “bias” current } plus { a net synaptic current }. Net synaptic current decays toward 0 with time constant taus, where taus > taum (synaptic current decays slowly compared to the rate at which “membrane potential” m equilibrates). When an input event with weight w arrives, the net synaptic current changes abruptly by the amount w.
-
class
IntFire4¶ ↑ - Syntax:
c = h.IntFire4()c.taue --- ms excitatory input time constantc.taui1 --- ms inhibitory input rise time constantc.taui2 --- ms inhibitory input fall time constantc.taum --- membrane time constantc.m --- membrane state variablec.M --- analytic value of membrane state at current time, tc.e --- excitatory current state variablec.E --- analytic value of excitation currentc.i1 c.i2 -- inhibitory current state variablesc.I --- analytic value of inhibitory current.- Description:
The IntFire4 artificial cell treats excitatory input (positive weight) events as a sudden change in current which decays exponentially with time constant taue. Inhibitory input (negative weight) events are treated as an alpha function like change to the current. More precisely the current due to a negative weight event is the difference between two exponentials with time constants taui1 and taui2. In the limit as taui2 approaches taui1 then the current due to the event approaches the alpha function. The current due to the input events is integrated with a membrane time constant of taum. At present there is a constraint taue < taui1 < taui2 < taum but this may become relaxed to taue, taui1 < taui2, taum. When the membrane potential reaches 1, the cell fires and the membrane potential is re-initialized to 0 and starts integrating according to the analytic value of the current (which does NOT depend on firing). Excitatory events are scaled such that an isolated event of weight 1 will produce a maximum membrane potential of 1 (threshold) and an isolated inhibitory event of weight -1 will produce a minimum membrane potential of -1.
Mechanisms¶ ↑
setdata
- Syntax:
h.setdata_suffix(section(x))- Description:
- If a mechanism function is called that uses RANGE variables, then the appropriate data needed by the function must first be indicated via a setdata call. This is unnecessary if the function uses only GLOBAL variables. The suffix refers to the name of the mechanism. E.g.
h.setdata_hh(soma(0.5)).Warning
The THREADSAFE mechanism case is a bit more complicated if the mechanism anywhere assigns a value to a GLOBAL variable. When the user explicitly specifies that a mechanism is THREADSAFE, those GLOBAL variables that anywhere appear on the left hand side of an assignment statement (and there is no such assignment with the PROTECT prefix) are actually thread specific variables. Hoc access to thread specific global variables is with respect to a static instance which is shared by the first thread in which mechanism actually exists.
capacitance
- Syntax:
section.cm (uF/cm2)
section.i_cap (mA/cm2)- Description:
- capacitance is a mechanism that automatically is inserted into every section. cm is a range variable with a default value of 1.0. i_cap is a range variable which contains the varying membrane capacitive current during a simulation. Note that i_cap is most accurate when a variable step integration method is used.
hh
- Syntax:
section.insert('hh')- Description:
See <nrn src dir>/src/nrnoc/hh.mod
Hodgkin-Huxley sodium, potassium, and leakage channels. Range variables specific to this model are:
hh.gnabarh 0.120 mho/cm2 Maximum specific sodium channel conductance hh.gkbar 0.036 mho/cm2 Maximum potassium channel conductance hh.gl 0.0003 mho/cm2 Leakage conductance hh.el -54.3 mV Leakage reversal potential hh.m sodium activation state variable hh.h sodium inactivation state variable hh.n potassium activation state variable hh.ina mA/cm2 sodium current through the hh channels hh.ik mA/cm2 potassium current through the hh channels h.rates_hh(v) computes the global variables [mhn]inf_hh and [mhn]tau_hh from the rate functions. usetable_hh defaults to 1.This model used the na and k ions to read ena, ek and write ina, ik.
pas
- Syntax:
section.insert('pas')
section.pas.g -- mho/cm2 conductance
section.pas.e -- mV reversal potential
section.pas.i -- mA/cm2 non-specific current- Description:
See <nrn src dir>/src/nrnoc/passive.mod
Passive membrane channel.
fastpas
See <nrn src dir>/src/nrnoc/passive0.c
Passive membrane channel. Same as the pas mechanism but hand coded to be a bit faster (avoids the wasteful numerical derivative computation of the conductance and does not save the current). Generally not worth using since passive channel computations are not usually the rate limiting step of a simulation.
extracellular
- Syntax:
section.insert('extracellular')
.vext[2] -- mV
.i_membrane -- mA/cm2
.xraxial[2] -- MOhms/cm
.xg[2] -- mho/cm2
.xc[2] -- uF/cm2
.extracellular.e -- mV- Description:
Adds two layers of extracellular field to the section. Vext is solved simultaneously with the v. When the extracellular mechanism is present, v refers to the membrane potential and vext (i.e. vext[0]) refers to the extracellular potential just next to the membrane. Thus the internal potential is v+vext (but see BUGS).
This mechanism is useful for simulating the stimulation with extracellular electrodes, response in the presence of an extracellular potential boundary condition computed by some external program, leaky patch clamps, incomplete seals in the myelin sheath along with current flow in the space between the myelin and the axon. It is required when connecting
LinearMechanism(e.g. a circuit built with the ) to extracellular nodes.i_membrane correctly does not include contributions from ELECTRODE_CURRENT point processes.
See i_membrane_ at
CVode.use_fast_imem().The figure illustrates the form the electrical equivalent circuit when this mechanism is present. Note that previous documentation was incorrect in showing that e_extracellular was in series with the
xg[nlayer-1],xc[nlayer-1]parallel combination. In fact it has always been the case that e_extracellular was in series with xg[nlayer-1] and xc[nlayer-1] was in parallel with that series combination.Note
The only reason the standard distribution is built with nlayer=2 is so that when only a single layer is needed (the usual case), then e_extracellular is consistent with the previous documentation with the old default nlayer=1.
e_extracellular is connected in series with the conductance of the last extracellular layer. With two layers the equivalent circuit looks like:
Ra o/`--o--'\/\/`--o--'\/\/`--o--'\/\/`--o--'\o vext + v | | | | --- --- --- --- | | | | | | | | --- --- --- --- | | | | | | | | i_membrane | xraxial | | | /`--o--'\/\/`--o--'\/\/`--o--'\/\/`--o--'vext | | | | --- --- --- --- xc and xg | | | | | | | | in parallel --- --- --- --- | | | | | | | | |xraxial[1]| | | /`--o--'\/\/`--o--'\/\/`--o--'\/\/`--o--'vext[1] | | | | --- --- --- --- the series xg[1], e_extracellular | | | | | | | | combination is in parallel with | --- | --- | --- | --- the xc[1] capacitance. This is | - | - | - | - identical to a membrane with --- --- --- --- cm, g_pas, e_pas | | | | -------------------------------------------- groundExtracellular potentials do a great deal of violence to one’s intuition and it is important that the user carefully consider the results of simulations that use them. It is best to start out believing that there are bugs in the method and attempt to prove their existence.
See <nrn src dir>/src/nrnoc/extcell.c and <nrn src dir>/examples/nrnoc/extcab*.hoc.
NEURON can be compiled with any number of extracellular layers. See below.
Warning
xcaxial is also defined but is not implemented. If you need those then add them with the
LinearMechanism.Prior versions of this document indicated that e_extracellular is in series with the parallel (xc,xg) pair. In fact it was in series with xg of the layer. The above equivalent circuit has been changed to reflect the truth about the implementation.
In v4.3.1 2000/09/06 and before vext(0) and vext(1) are the voltages at the centers of the first and last segments instead of the zero area nodes.
Now the above bug is fixed and vext(0) and vext(1) are the voltages at the zero area nodes.
From extcell.c the comment is:
i_membrane = sav_g * ndlist[i]->v + sav_rhs; #if 1 /* i_membrane is a current density (mA/cm2). However it contains contributions from Non-ELECTRODE_CURRENT point processes. i_membrane(0) and i_membrane(1) will return the membrane current density at the points 0.5/nseg and 1-0.5/nseg respectively. This can cause confusion if non-ELECTRODE_CURRENT point processes are located at these 0-area nodes since 1) not only is the true current density infinite, but 2) the correct absolute current is being computed here at the x=1 point but is not available, and 3) the correct absolute current at x=0 is not computed if the parent is a rootnode or there is no extracellular mechanism for the parent of this section. Thus, if non-ELECTRODE_CURRENT point processes eg synapses, are being used it is not a good idea to insert them at the points x=0 or x=1 */ #else i_membrane *= ndlist[i]->area; /* i_membrane is nA for every segment. This is different from all other continuous mechanism currents and same as PointProcess currents since it contains non-ELECTRODE_CURRENT point processes and may be non-zero for the zero area nodes. */ #endifIn v4.3.1 2000/09/06 and before extracellular layers will not be connected across sections unless the parent section of the connection contains the extracellular mechanism. This is because the 0 area node of the connection is “owned” by the parent section. In particular, root nodes never contain extracellular mechanisms and thus multiple sections connected to the root node always appear to be extracellularly disconnected. This bug has been fixed. However it is still the case that vext(0) can be non-zero only if the section owning the 0 node has had the extracellular mechanism inserted. It is best to have every section in a cell contain the extracellular mechanism if any one of them does to avoid confusion with regard to (the in fact correct) boundary conditions.
- Syntax:
nrn/src/nrnoc/options.h
#define EXTRACELLULAR 2 /* number of extracellular layers */
section.insert('extracellular')
.vext[i] -- mV
.i_membrane -- mA/cm2
.xraxial[i] -- MOhms/cm
.xg[i] -- mho/cm2
.xc[i] -- uF/cm2
.extracellular.e -- mV- Description:
If other than 2 extracellular layers is desired, you may recompile the program by changing the
nrn/src/nrnoc/options.hline#define EXTRACELLULAR 2to the number of layers desired. Be sure to recompile both nrnoc and nrniv as well as any user defined .mod files that use the ELECTRODE_CURRENT statement.Note that vext is a synonym in hoc for vext[0]. Since the default value for xg[i] = 1e9 all layers start out tightly connected to ground so previous single layer extracellular simulations should produce the same results if either xc or e_extracellular was 0.
extracellular.e is connected in series with the conductance of the last extracellular layer.