Ball-and-stick: 2 - Cell class¶
This page is the second in a series where we build a multicompartment cell and evolve it into a network of cells running on a parallel machine. In this page, we encapsulate much of the functionality of the previous page into Python functions and class objects. When code is encapsulated into a class, it can be represented as an object with particular functionality. As a Python object, it can be replicated many times. That is, multiple instances of the object can exist in the program. Therefore, cells make great examples of objects, especially when multiple cells are used in a network.
Ball and stick class¶
From the previous lesson, we saw that cell objects have the following components:
- Sections - the cell sections.
- Topology - The connectivity of the sections
- Geometry - The 3D location of the sections
- Biophysics - The ionic channels and membrane properties of the sections
- Synapses - Optional list of synapses onto the cell.
With this in mind, let’s encapsulate these concepts in the class’s methods. Let’s first start with imports used in the previous worksheet and import them here.
import numpy
from matplotlib import pyplot
from neuron import h, gui
Recall
On the previous page, we constructed a single ball and stick cell via:
# Create sections
soma = h.Section(name='soma')
dend = h.Section(name='dend')
# Topology
dend.connect(soma(1))
# Geometry
soma.L = soma.diam = 12.6157 # microns
dend.L = 200 # microns
dend.diam = 1 # microns
h.define_shape() # Translate into 3D points.
# Biophysics
for sec in h.allsec():
sec.Ra = 100 # Axial resistance in Ohm * cm
sec.cm = 1 # Membrane capacitance in micro Farads / cm^2
# Insert active Hodgkin-Huxley current in the soma
soma.insert('hh')
for seg in soma:
seg.hh.gnabar = 0.12 # Sodium conductance in S/cm2
seg.hh.gkbar = 0.036 # Potassium conductance in S/cm2
seg.hh.gl = 0.0003 # Leak conductance in S/cm2
seg.hh.el = -54.3 # Reversal potential in mV
# Insert passive current in the dendrite
dend.insert('pas')
for seg in dend:
seg.pas.g = 0.001 # Passive conductance in S/cm2
seg.pas.e = -65 # Leak reversal potential mV
We can make arbitrarily many copies of the cell by building it inside of a class.
(In particular, the rest of this page assumes that the code in the recall block
has not been run.)
Instead of calling a section soma, we will now call it self.soma to indicate
to which cell it belongs. Additionally, note the build_subsets() method and how ‘all’ is used.
The use of a SectionList instead of a Python list allows us to locate the whole neuron no matter how complicated in one line based on the connectivity.
Finally, note that we split the conceptual steps of describing the cell to be simulated into separate
methods to clarify the purpose of each code block.
class BallAndStick(object):
"""Two-section cell: A soma with active channels and
a dendrite with passive properties."""
def __init__(self):
self.create_sections()
self.build_topology()
self.build_subsets()
self.define_geometry()
self.define_biophysics()
#
def create_sections(self):
"""Create the sections of the cell."""
# NOTE: cell=self is required to tell NEURON of this object.
self.soma = h.Section(name='soma', cell=self)
self.dend = h.Section(name='dend', cell=self)
#
def build_topology(self):
"""Connect the sections of the cell to build a tree."""
self.dend.connect(self.soma(1))
#
def define_geometry(self):
"""Set the 3D geometry of the cell."""
self.soma.L = self.soma.diam = 12.6157 # microns
self.dend.L = 200 # microns
self.dend.diam = 1 # microns
self.dend.nseg = 5
h.define_shape() # Translate into 3D points.
#
def define_biophysics(self):
"""Assign the membrane properties across the cell."""
for sec in self.all: # 'all' defined in build_subsets
sec.Ra = 100 # Axial resistance in Ohm * cm
sec.cm = 1 # Membrane capacitance in micro Farads / cm^2
# Insert active Hodgkin-Huxley current in the soma
self.soma.insert('hh')
for seg in self.soma:
seg.hh.gnabar = 0.12 # Sodium conductance in S/cm2
seg.hh.gkbar = 0.036 # Potassium conductance in S/cm2
seg.hh.gl = 0.0003 # Leak conductance in S/cm2
seg.hh.el = -54.3 # Reversal potential in mV
# Insert passive current in the dendrite
self.dend.insert('pas')
for seg in self.dend:
seg.pas.g = 0.001 # Passive conductance in S/cm2
seg.pas.e = -65 # Leak reversal potential mV
#
def build_subsets(self):
"""Build subset lists. For now we define 'all'."""
self.all = h.SectionList()
self.all.wholetree(sec=self.soma)
Note
The # signs separating each method in the class are unnecessary when
running the code as a script. They are included here to allow this code-block
to be copy-pasted into a Python console. (Without them, Python would interpret
a blank line as indicating the end of the class.)
Let’s make an instance of the cell.
cell = BallAndStick()
Success? Let’s look.
h.psection(sec=cell.dend)
So far so good. Let’s now attach a stimulator, run the simulation and see how it looks.
def attach_current_clamp(cell, delay=5, dur=1, amp=.1, loc=1):
"""Attach a current Clamp to a cell.
:param cell: Cell object to attach the current clamp.
:param delay: Onset of the injected current.
:param dur: Duration of the stimulus.
:param amp: Magnitude of the current.
:param loc: Location on the dendrite where the stimulus is placed.
"""
stim = h.IClamp(cell.dend(loc))
stim.delay = delay
stim.dur = dur
stim.amp = amp
return stim
def set_recording_vectors(cell):
"""Set soma, dendrite, and time recording vectors on the cell.
:param cell: Cell to record from.
:return: the soma, dendrite, and time vectors as a tuple.
"""
soma_v_vec = h.Vector() # Membrane potential vector at soma
dend_v_vec = h.Vector() # Membrane potential vector at dendrite
t_vec = h.Vector() # Time stamp vector
soma_v_vec.record(cell.soma(0.5)._ref_v)
dend_v_vec.record(cell.dend(0.5)._ref_v)
t_vec.record(h._ref_t)
return soma_v_vec, dend_v_vec, t_vec
def simulate(tstop=25):
"""Initialize and run a simulation.
:param tstop: Duration of the simulation.
"""
h.tstop = tstop
h.run()
def show_output(soma_v_vec, dend_v_vec, t_vec, new_fig=True):
"""Draw the output.
:param soma_v_vec: Membrane potential vector at the soma.
:param dend_v_vec: Membrane potential vector at the dendrite.
:param t_vec: Timestamp vector.
:param new_fig: Flag to create a new figure (and not draw on top
of previous results)
"""
if new_fig:
pyplot.figure(figsize=(8,4)) # Default figsize is (8,6)
soma_plot = pyplot.plot(t_vec, soma_v_vec, color='black')
dend_plot = pyplot.plot(t_vec, dend_v_vec, color='red')
pyplot.legend(soma_plot + dend_plot, ['soma', 'dend(0.5)'])
pyplot.xlabel('time (ms)')
pyplot.ylabel('mV')
stim = attach_current_clamp(cell)
soma_v_vec, dend_v_vec, t_vec = set_recording_vectors(cell)
simulate()
show_output(soma_v_vec, dend_v_vec, t_vec)
pyplot.show()
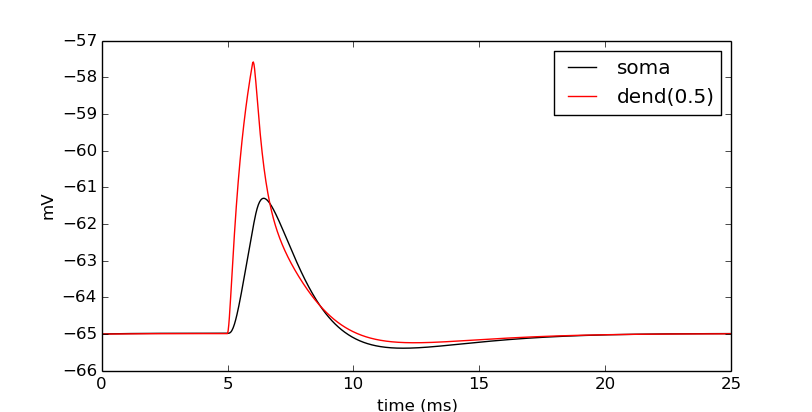
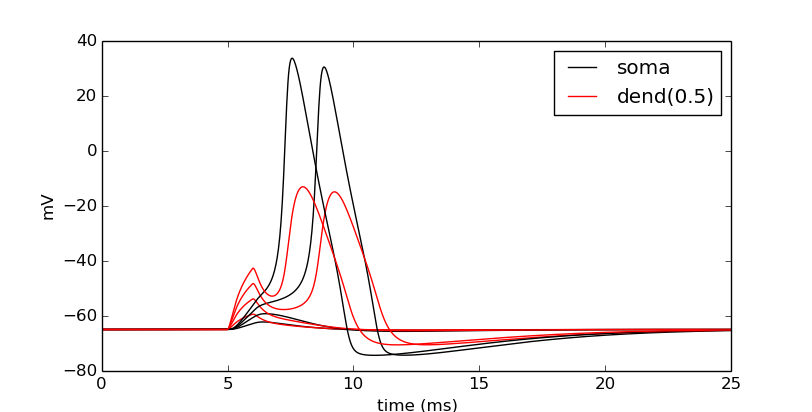
Now let’s compare the effects of four different current strengths:
step = 0.075
num_steps = 4
for i in numpy.linspace(step, step*num_steps, num_steps):
stim.amp = i
simulate()
# When i==step, we are at the first time through.
show_output(soma_v_vec, dend_v_vec, t_vec, i==step)
pyplot.show()
Aside: Docstrings¶
You may have wondered why our functions begin with a triple-quoted string
describing their purpose. These strings are known as docstrings. Like normal
comments, they make it easier to understand code that you have not looked
at recently. Python’s help() displays these strings when the user
asks for help about the functions. Documentation generators use them to
automatically generate documentation from the source code. The markup used
to indicate parameters and return values in these examples is understood by
the Sphinx documentation generator.
This concludes this part of the tutorial. On the next page, we will make a ring network of ball-and-stick cells.